BlackBody

class astropy.modeling.physical_models.BlackBody(*args, **kwargs)

Bases: Fittable1DModel

Blackbody model using the Planck function.

Parameters:

temperatureQuantity [:ref: ‘temperature’]

Blackbody temperature.

scalefloat or Quantity [:ref: ‘dimensionless’]

Scale factor. If dimensionless, input units will assumed to be in Hz and output units in (erg / (cm ** 2 * s * Hz * sr). If not dimensionless, must be equivalent to either (erg / (cm ** 2 * s * Hz * sr) or erg / (cm ** 2 * s * AA * sr), in which case the result will be returned in the requested units and the scale will be stripped of units (with the float value applied).

Notes

Model formula:

\[B_{\nu}(T) = A \frac{2 h \nu^{3} / c^{2}}{exp(h \nu / k T) - 1}\]

Examples

>>> from astropy.modeling import models
>>> from astropy import units as u
>>> bb = models.BlackBody(temperature=5000*u.K)
>>> bb(6000 * u.AA)  
<Quantity 1.53254685e-05 erg / (Hz s sr cm2)>

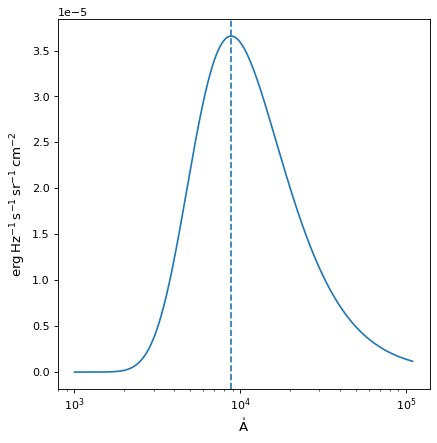
import numpy as np
import matplotlib.pyplot as plt

from astropy.modeling.models import BlackBody
from astropy import units as u
from astropy.visualization import quantity_support

bb = BlackBody(temperature=5778*u.K)
wav = np.arange(1000, 110000) * u.AA
flux = bb(wav)

with quantity_support():
    plt.figure()
    plt.semilogx(wav, flux)
    plt.axvline(bb.nu_max.to(u.AA, equivalencies=u.spectral()).value, ls='--')
    plt.show()

(png, svg, pdf)

Attributes Summary

bolometric_flux	Bolometric flux.
input_units	This property is used to indicate what units or sets of units the evaluate method expects, and returns a dictionary mapping inputs to units (or None if any units are accepted).
input_units_equivalencies
lambda_max	Peak wavelength when the curve is expressed as power density.
nu_max	Peak frequency when the curve is expressed as power density.
param_names	Names of the parameters that describe models of this type.
scale
temperature

Methods Summary

evaluate(x, temperature, scale)

Evaluate the model.

Attributes Documentation

bolometric_flux

Bolometric flux.

input_units

input_units_equivalencies = {'x': [(Unit("m"), Unit("Hz"), <function spectral.<locals>.<lambda>>), (Unit("m"), Unit("J"), <function spectral.<locals>.<lambda>>), (Unit("Hz"), Unit("J"), <function spectral.<locals>.<lambda>>, <function spectral.<locals>.<lambda>>), (Unit("m"), Unit("1 / m"), <function spectral.<locals>.<lambda>>), (Unit("Hz"), Unit("1 / m"), <function spectral.<locals>.<lambda>>, <function spectral.<locals>.<lambda>>), (Unit("J"), Unit("1 / m"), <function spectral.<locals>.<lambda>>, <function spectral.<locals>.<lambda>>), (Unit("1 / m"), Unit("rad / m"), <function spectral.<locals>.<lambda>>, <function spectral.<locals>.<lambda>>), (Unit("m"), Unit("rad / m"), <function spectral.<locals>.<lambda>>), (Unit("Hz"), Unit("rad / m"), <function spectral.<locals>.<lambda>>, <function spectral.<locals>.<lambda>>), (Unit("J"), Unit("rad / m"), <function spectral.<locals>.<lambda>>, <function spectral.<locals>.<lambda>>)]}

lambda_max

Peak wavelength when the curve is expressed as power density.

nu_max

Peak frequency when the curve is expressed as power density.

param_names = ('temperature', 'scale')

Names of the parameters that describe models of this type.

The parameters in this tuple are in the same order they should be passed in when initializing a model of a specific type. Some types of models, such as polynomial models, have a different number of parameters depending on some other property of the model, such as the degree.

When defining a custom model class the value of this attribute is automatically set by the Parameter attributes defined in the class body.

scale = Parameter('scale', value=1.0, bounds=(0, None))

temperature = Parameter('temperature', value=5000.0, unit=K, bounds=(0, None))

Methods Documentation

evaluate(x, temperature, scale)

Evaluate the model.

Parameters:

xfloat, ndarray, or Quantity [:ref: ‘frequency’]

Frequency at which to compute the blackbody. If no units are given, this defaults to Hz (or AA if scale was initialized with units equivalent to erg / (cm ** 2 * s * AA * sr)).

temperaturefloat, ndarray, or Quantity

Temperature of the blackbody. If no units are given, this defaults to Kelvin.

scalefloat, ndarray, or Quantity [:ref: ‘dimensionless’]

Desired scale for the blackbody.

Returns:

ynumber or ndarray

Blackbody spectrum. The units are determined from the units of scale.

Note

Use numpy.errstate to suppress Numpy warnings, if desired.

Raises:

ValueError

Invalid temperature.

ZeroDivisionError

Wavelength is zero (when converting to frequency).