Models#
Basics#
The astropy.modeling package defines a number of models that are collected
under a single namespace as astropy.modeling.models. Models behave like
parametrized functions:
>>> import numpy as np
>>> from astropy.modeling import models
>>> g = models.Gaussian1D(amplitude=1.2, mean=0.9, stddev=0.5)
>>> print(g)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Parameters:
amplitude mean stddev
--------- ---- ------
1.2 0.9 0.5
Model parameters can be accessed as attributes:
>>> g.amplitude
Parameter('amplitude', value=1.2)
>>> g.mean
Parameter('mean', value=0.9)
>>> g.stddev
Parameter('stddev', value=0.5, bounds=(1.1754943508222875e-38, None))
and can also be updated via those attributes:
>>> g.amplitude = 0.8
>>> g.amplitude
Parameter('amplitude', value=0.8)
Models can be evaluated by calling them as functions:
>>> g(0.1)
0.22242984036255528
>>> g(np.linspace(0.5, 1.5, 7))
array([0.58091923, 0.71746405, 0.7929204 , 0.78415894, 0.69394278,
0.54952605, 0.3894018 ])
As the above example demonstrates, in general most models evaluate array-like inputs according to the standard Numpy broadcasting rules for arrays. Models can therefore already be useful to evaluate common functions, independently of the fitting features of the package.
Instantiating and Evaluating Models#
In general, models are instantiated by supplying the parameter values that define that instance of the model to the constructor, as demonstrated in the section on Parameters.
Additionally, a Model instance may represent a single model
with one set of parameters, or a Model set consisting
of a set of parameters each representing a different parameterization of the same
parametric model. For example, you may instantiate a single Gaussian model
with one mean, standard deviation, and amplitude. Or you may create a set
of N Gaussians, each one of which would be evaluated on, for example, a
different plane in an image cube.
For example, a single Gaussian model may be instantiated with all scalar parameters:
>>> from astropy.modeling.models import Gaussian1D
>>> g = Gaussian1D(amplitude=1, mean=0, stddev=1)
>>> g
<Gaussian1D(amplitude=1., mean=0., stddev=1.)>
The newly created model instance g now works like a Gaussian function
with the specific parameters. It takes a single input:
>>> g.inputs
('x',)
>>> g(x=0)
1.0
The model can also be called without explicitly using keyword arguments:
>>> g(0)
1.0
Or a set of Gaussians may be instantiated by passing multiple parameter values:
>>> from astropy.modeling.models import Gaussian1D
>>> gset = Gaussian1D(amplitude=[1, 1.5, 2],
... mean=[0, 1, 2],
... stddev=[1., 1., 1.],
... n_models=3)
>>> print(gset)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 3
Parameters:
amplitude mean stddev
--------- ---- ------
1.0 0.0 1.0
1.5 1.0 1.0
2.0 2.0 1.0
This model also works like a Gaussian function. The three models in the model set can be evaluated on the same input:
>>> gset(1.)
array([0.60653066, 1.5 , 1.21306132])
or on N=3 inputs:
>>> gset([1, 2, 3])
array([0.60653066, 0.90979599, 1.21306132])
For a comprehensive example of fitting a model set see Fitting Model Sets.
Model inverses#
All models have a Model.inverse property
which may, for some models, return a new model that is the analytic inverse of
the model it is attached to. For example:
>>> from astropy.modeling.models import Linear1D
>>> linear = Linear1D(slope=0.8, intercept=1.0)
>>> linear.inverse
<Linear1D(slope=1.25, intercept=-1.25)>
The inverse of a model will always be a fully instantiated model in its own right, and so can be evaluated directly like:
>>> linear.inverse(2.0)
1.25
It is also possible to assign a custom inverse to a model. This may be useful, for example, in cases where a model does not have an analytic inverse, but may have an approximate inverse that was computed numerically and is represented by another model. This works even if the target model has a default analytic inverse–in this case the default is overridden with the custom inverse:
>>> from astropy.modeling.models import Polynomial1D
>>> linear.inverse = Polynomial1D(degree=1, c0=-1.25, c1=1.25)
>>> linear.inverse
<Polynomial1D(1, c0=-1.25, c1=1.25)>
If a custom inverse has been assigned to a model, it can be deleted with
del model.inverse. This resets the inverse to its default (if one exists).
If a default does not exist, accessing model.inverse raises a
NotImplementedError. For example polynomial models do not have a default
inverse:
>>> del linear.inverse
>>> linear.inverse
<Linear1D(slope=1.25, intercept=-1.25)>
>>> p = Polynomial1D(degree=2, c0=1.0, c1=2.0, c2=3.0)
>>> p.inverse
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "astropy\modeling\core.py", line 796, in inverse
raise NotImplementedError("An analytical inverse transform has not "
NotImplementedError: No analytical or user-supplied inverse transform
has been implemented for this model.
One may certainly compute an inverse and assign it to a polynomial model though.
Note
When assigning a custom inverse to a model no validation is performed to ensure that it is actually an inverse or even approximate inverse. So assign custom inverses at your own risk.
Bounding Boxes#
Efficient Model Rendering with Bounding Boxes#
All Model subclasses have a
bounding_box attribute that
can be used to set the limits over which the model is significant. This greatly
improves the efficiency of evaluation when the input range is much larger than
the characteristic width of the model itself. For example, to create a sky model
image from a large survey catalog, each source should only be evaluated over the
pixels to which it contributes a significant amount of flux. This task can
otherwise be computationally prohibitive on an average CPU.
The Model.render method can be used to
evaluate a model on an output array, or input coordinate arrays, limiting the
evaluation to the bounding_box region if
it is set. This function will also produce postage stamp images of the model if
no other input array is passed. To instead extract postage stamps from the data
array itself, see 2D Cutout Images.
Using the standard Bounding Box#
For basic usage, see Model.bounding_box.
By default no bounding_box is set, except on model
subclasses where a bounding_box property or method is explicitly defined.
The default is then the minimum rectangular region symmetric about the position
that fully contains the model. If the model does not have a finite extent,
the containment criteria are noted in the documentation. For example, see
Gaussian2D.bounding_box.
Warning
Accessing the Model.bounding_box
property when it has not been set, or does not have a default will
result in a NotImplementedError. If this behavior is undesirable,
then one can instead use the Model.get_bounding_box
method instead. This method will return the bounding box if one exists
(by setting or default) otherwise it will return None instead
of raising an error.
A Model.bounding_box default can be
set by the user to any callable. This is particularly useful for models created
with custom_model or as a CompoundModel:
>>> from astropy.modeling import custom_model
>>> def ellipsoid(x, y, z, x0=0, y0=0, z0=0, a=2, b=3, c=4, amp=1):
... rsq = ((x - x0) / a) ** 2 + ((y - y0) / b) ** 2 + ((z - z0) / c) ** 2
... val = (rsq < 1) * amp
... return val
...
>>> class Ellipsoid3D(custom_model(ellipsoid)):
... # A 3D ellipsoid model
... def bounding_box(self):
... return ((self.z0 - self.c, self.z0 + self.c),
... (self.y0 - self.b, self.y0 + self.b),
... (self.x0 - self.a, self.x0 + self.a))
...
>>> model1 = Ellipsoid3D()
>>> model1.bounding_box
ModelBoundingBox(
intervals={
x0: Interval(lower=-2.0, upper=2.0)
x1: Interval(lower=-3.0, upper=3.0)
x2: Interval(lower=-4.0, upper=4.0)
}
model=Ellipsoid3D(inputs=('x0', 'x1', 'x2'))
order='C'
)
By default models are evaluated on any inputs. By passing a flag they can be evaluated
only on inputs within the bounding box. For inputs outside of the bounding_box a fill_value is
returned (np.nan by default):
>>> model1(-5, 1, 1)
0.0
>>> model1(-5, 1, 1, with_bounding_box=True)
nan
>>> model1(-5, 1, 1, with_bounding_box=True, fill_value=-1)
-1.0
Model.bounding_box can be set on any
model instance via the usage of the property setter. For example for a single
input model one needs to only set a tuple of the lower and upper bounds
>>> from astropy.modeling.models import Polynomial1D
>>> model2 = Polynomial1D(2)
>>> model2.bounding_box = (-1, 1)
>>> model2.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
}
model=Polynomial1D(inputs=('x',))
order='C'
)
>>> model2(-2)
0.0
>>> model2(-2, with_bounding_box=True)
nan
>>> model2(-2, with_bounding_box=True, fill_value=47)
47.0
For multi-input models, Model.bounding_box
can be set on any model instance by specifying a tuple of lower/upper bound tuples
>>> from astropy.modeling.models import Polynomial2D
>>> model3 = Polynomial2D(2)
>>> model3.bounding_box = ((-2, 2), (-1, 1))
>>> model3.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
y: Interval(lower=-2, upper=2)
}
model=Polynomial2D(inputs=('x', 'y'))
order='C'
)
>>> model3(-2, 0)
0.0
>>> model3(-2, 0, with_bounding_box=True)
nan
>>> model3(-2, 0, with_bounding_box=True, fill_value=7)
7.0
Note that if one wants to directly recover the tuple used to formulate
a bounding box, then one can use the
ModelBoundingBox.bounding_box()
method
>>> model1.bounding_box.bounding_box()
((-4.0, 4.0), (-3.0, 3.0), (-2.0, 2.0))
>>> model2.bounding_box.bounding_box()
(-1, 1)
>>> model3.bounding_box.bounding_box()
((-2, 2), (-1, 1))
Warning
When setting multi-dimensional bounding boxes it is important to
remember that by default the tuple of tuples is assumed to be 'C' ordered,
which means that the bound tuples will be ordered in the reverse order
to their respective input order. That is if the inputs are in the order
('x', 'y', 'z') then the bounds will need to be listed in ('z', 'y', 'x')
order.
The if one does not want to work directly with the default 'C' ordered
bounding boxes. It is possible to use the alternate 'F' ordering, which
orders the bounding box tuple in the same order as the inputs. To do this
one can use the bind_bounding_box
function, and passing the order='F' keyword argument
>>> from astropy.modeling import bind_bounding_box
>>> model4 = Polynomial2D(3)
>>> bind_bounding_box(model4, ((-1, 1), (-2, 2)), order='F')
>>> model4.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
y: Interval(lower=-2, upper=2)
}
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
>>> model4(-2, 0)
0.0
>>> model4(-2, 0, with_bounding_box=True)
nan
>>> model4(-2, 0, with_bounding_box=True, fill_value=12)
12.0
>>> model4.bounding_box.bounding_box()
((-1, 1), (-2, 2))
>>> model4.bounding_box.bounding_box(order='C')
((-2, 2), (-1, 1))
Warning
Currently when combining models the bounding boxes of components are
combined only when joining models with the & operator.
For the other operators bounding boxes for compound models must be assigned
explicitly. A future release will determine the appropriate bounding box
for a compound model where possible.
Using the Compound Bounding Box#
Sometimes it is useful to have multiple bounding boxes for the same model,
which are selectable when the model is evaluated. In this case, one should
consider using a CompoundBoundingBox.
A common use case for this may be if the model has a single “discrete”
selector input (for example 'slit_id'), which among other things,
determines what bounding box should be applied to the other inputs. To
do this one needs to first define a dictionary of bounding box tuples,
with dictionary keys being the specific values of the selector input
corresponding to that specific bounding box
>>> from astropy.modeling.models import Shift, Identity
>>> model1 = Shift(1) & Shift(2) & Identity(1)
>>> model1.inputs = ('x', 'y', 'slit_id')
>>> bboxes = {
... 0: ((0, 1), (1, 2)),
... 1: ((2, 3), (3, 4))
... }
In order for the compound bounding box to function one must specify a list of selector arguments, where the elements of this list are tuples of the input’s name and whether or not the bounding box should be applied to the selector argument or not. In this case, it makes sense for the selector argument to be ignored
>>> from astropy.modeling.core import bind_compound_bounding_box
>>> selector_args = [('slit_id', True)]
>>> bind_compound_bounding_box(model1, bboxes, selector_args, order='F')
>>> model1.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0,) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
y: Interval(lower=1, upper=2)
}
ignored=['slit_id']
model=CompoundModel(inputs=('x', 'y', 'slit_id'))
order='F'
)
(1,) = ModelBoundingBox(
intervals={
x: Interval(lower=2, upper=3)
y: Interval(lower=3, upper=4)
}
ignored=['slit_id']
model=CompoundModel(inputs=('x', 'y', 'slit_id'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='slit_id', ignore=True)
)
)
>>> model1(0.5, 1.5, 0, with_bounding_box=True)
(1.5, 3.5, 0.0)
>>> model1(0.5, 1.5, 1, with_bounding_box=True)
(nan, nan, nan)
Multiple selector arguments can also be used, in this case the keys of the dictionary of bounding boxes need to be specified as tuples of values
>>> model2 = Shift(1) & Shift(2) & Identity(2)
>>> model2.inputs = ('x', 'y', 'slit_x', 'slit_y')
>>> bboxes = {
... (0, 0): ((0, 1), (1, 2)),
... (0, 1): ((2, 3), (3, 4)),
... (1, 0): ((4, 5), (5, 6)),
... (1, 1): ((6, 7), (7, 8)),
... }
>>> selector_args = [('slit_x', True), ('slit_y', True)]
>>> bind_compound_bounding_box(model2, bboxes, selector_args, order='F')
>>> model2.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0, 0) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
y: Interval(lower=1, upper=2)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
(0, 1) = ModelBoundingBox(
intervals={
x: Interval(lower=2, upper=3)
y: Interval(lower=3, upper=4)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
(1, 0) = ModelBoundingBox(
intervals={
x: Interval(lower=4, upper=5)
y: Interval(lower=5, upper=6)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
(1, 1) = ModelBoundingBox(
intervals={
x: Interval(lower=6, upper=7)
y: Interval(lower=7, upper=8)
}
ignored=['slit_x', 'slit_y']
model=CompoundModel(inputs=('x', 'y', 'slit_x', 'slit_y'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='slit_x', ignore=True)
Argument(name='slit_y', ignore=True)
)
)
>>> model2(0.5, 1.5, 0, 0, with_bounding_box=True)
(1.5, 3.5, 0.0, 0.0)
>>> model2(0.5, 1.5, 1, 1, with_bounding_box=True)
(nan, nan, nan, nan)
Note that one can also specify the ordering for all the bounding boxes
comprising the compound bounding using the order keyword argument.
Another use case for this maybe a if one wants to use multiple bounding boxes for the same model, where the user chooses the bounding box when evaluating the model. In this case, one must still choose a selector argument as a fall back default for bounding box selection; however, this argument should not be ignored by the bounding box:
>>> from astropy.modeling.models import Polynomial2D
>>> from astropy.modeling import bind_compound_bounding_box
>>> model = Polynomial2D(3)
>>> bboxes = {
... 0: ((0, 1), (1, 2)),
... 1: ((2, 3), (3, 4))
... }
>>> selector_args = [('x', False)]
>>> bind_compound_bounding_box(model, bboxes, selector_args, order='F')
>>> model.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0,) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
y: Interval(lower=1, upper=2)
}
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
(1,) = ModelBoundingBox(
intervals={
x: Interval(lower=2, upper=3)
y: Interval(lower=3, upper=4)
}
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='x', ignore=False)
)
)
For the user to select the bounding box on evaluation, instead of
specifying, with_bounding_box=True as the keyword argument; the user
instead specifies with_bounding_box=<bounding_key>
>>> model(0.5, 1.5, with_bounding_box=0)
0.0
>>> model(0.5, 1.5, with_bounding_box=1)
nan
Ignoring Inputs in Bounding Boxes#
Both standard bounding box
and CompoundBoundingBox
support ignoring specific inputs from enforcement by the bounding box. Effectively,
for multi-dimensional models one can define bounding boxes so that bounds are
only applied to a subset of the model’s inputs rather than the default of enforcing
a bound of some kind on every input. Note that use of this feature is equivalent
to defining the bounds for an input to be [-np.inf, np.inf].
Warning
The ignored input feature is not available when constructing/adding bounding
boxes to models using tuples and the property interface. That is one cannot
ignore inputs when setting bounding boxes using model.bounding_box = (-1, 1).
This feature is only available via the methods
bind_bounding_box and
bind_compound_bounding_box.
Ignoring inputs for a bounding box can be achieved via passing a list of the input
name strings to be ignored to the ignored keyword argument in any of the main
bounding box interfaces.
>>> from astropy.modeling.models import Polynomial1D
>>> from astropy.modeling import bind_bounding_box
>>> model1 = Polynomial2D(3)
>>> bind_bounding_box(model1, {'x': (-1, 1)}, ignored=['y'])
>>> model1.bounding_box
ModelBoundingBox(
intervals={
x: Interval(lower=-1, upper=1)
}
ignored=['y']
model=Polynomial2D(inputs=('x', 'y'))
order='C'
)
>>> model1(-2, 0, with_bounding_box=True)
nan
>>> model1(0, 300, with_bounding_box=True)
0.0
Similarly, the ignored inputs will be applied to all of the bounding boxes contained within a compound bounding box.
>>> from astropy.modeling import bind_compound_bounding_box
>>> model2 = Polynomial2D(3)
>>> bboxes = {
... 0: {'x': (0, 1)},
... 1: {'x': (1, 2)}
... }
>>> selector_args = [('x', False)]
>>> bind_compound_bounding_box(model2, bboxes, selector_args, ignored=['y'], order='F')
>>> model2.bounding_box
CompoundBoundingBox(
bounding_boxes={
(0,) = ModelBoundingBox(
intervals={
x: Interval(lower=0, upper=1)
}
ignored=['y']
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
(1,) = ModelBoundingBox(
intervals={
x: Interval(lower=1, upper=2)
}
ignored=['y']
model=Polynomial2D(inputs=('x', 'y'))
order='F'
)
}
selector_args = SelectorArguments(
Argument(name='x', ignore=False)
)
)
>>> model2(0.5, 300, with_bounding_box=0)
0.0
>>> model2(0.5, 300, with_bounding_box=1)
nan
Efficient evaluation with Model.render()#
When a model is evaluated over a range much larger than the model itself, it
may be prudent to use the Model.render
method if efficiency is a concern. The render
method can be used to evaluate the model on an
array of the same dimensions. model.render() can be called with no
arguments to return a “postage stamp” of the bounding box region.
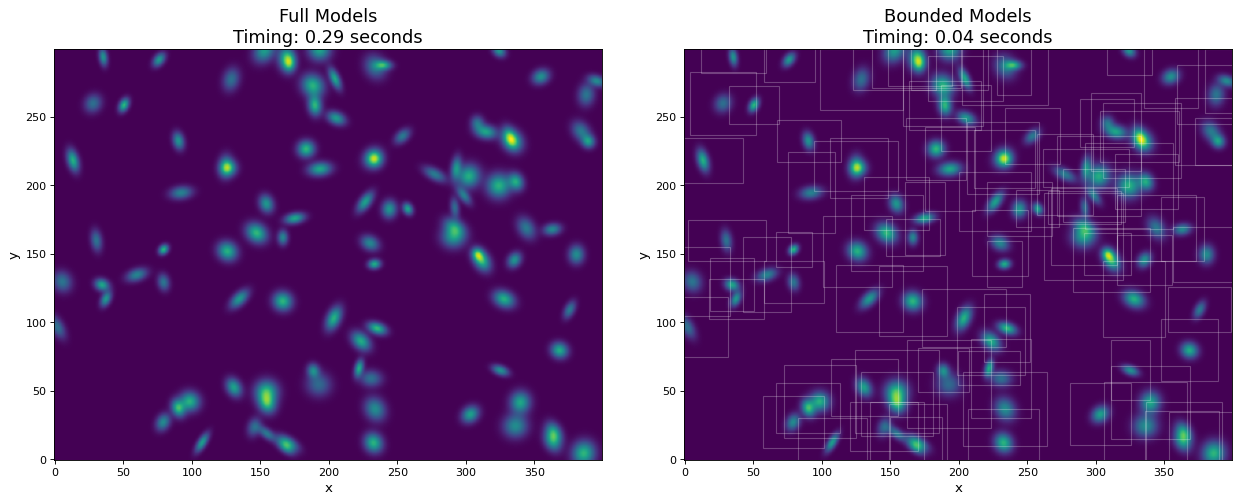
In this example, we generate a 300x400 pixel image of 100 2D Gaussian sources. For comparison, the models are evaluated both with and without using bounding boxes. By using bounding boxes, the evaluation speed increases by approximately a factor of 10 with negligible loss of information.
import numpy as np
from time import time
from astropy.modeling import models
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
imshape = (300, 400)
y, x = np.indices(imshape)
# Generate random source model list
rng = np.random.default_rng(0)
nsrc = 100
model_params = [
dict(amplitude=rng.uniform(.5, 1),
x_mean=rng.uniform(0, imshape[1] - 1),
y_mean=rng.uniform(0, imshape[0] - 1),
x_stddev=rng.uniform(2, 6),
y_stddev=rng.uniform(2, 6),
theta=rng.uniform(0, 2 * np.pi))
for _ in range(nsrc)]
model_list = [models.Gaussian2D(**kwargs) for kwargs in model_params]
# Render models to image using bounding boxes
bb_image = np.zeros(imshape)
t_bb = time()
for model in model_list:
model.render(bb_image)
t_bb = time() - t_bb
# Render models to image using full evaluation
full_image = np.zeros(imshape)
t_full = time()
for model in model_list:
model.bounding_box = None
model.render(full_image)
t_full = time() - t_full
flux = full_image.sum()
diff = (full_image - bb_image)
max_err = diff.max()
# Plots
plt.figure(figsize=(16, 7))
plt.subplots_adjust(left=.05, right=.97, bottom=.03, top=.97, wspace=0.15)
# Full model image
plt.subplot(121)
plt.imshow(full_image, origin='lower')
plt.title(f'Full Models\nTiming: {t_full:.2f} seconds', fontsize=16)
plt.xlabel('x')
plt.ylabel('y')
# Bounded model image with boxes overplotted
ax = plt.subplot(122)
plt.imshow(bb_image, origin='lower')
for model in model_list:
del model.bounding_box # Reset bounding_box to its default
dy, dx = np.diff(model.bounding_box).flatten()
pos = (model.x_mean.value - dx / 2, model.y_mean.value - dy / 2)
r = Rectangle(pos, dx, dy, edgecolor='w', facecolor='none', alpha=.25)
ax.add_patch(r)
plt.title(f'Bounded Models\nTiming: {t_bb:.2f} seconds', fontsize=16)
plt.xlabel('x')
plt.ylabel('y')
# Difference image
plt.figure(figsize=(16, 8))
plt.subplot(111)
plt.imshow(diff, vmin=-max_err, vmax=max_err)
plt.colorbar(format='%.1e')
plt.title(f'Difference Image\nTotal Flux Err = {((flux - np.sum(bb_image)) / flux):.0e}')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Model Separability#
Simple models have a boolean Model.separable property.
It indicates whether the outputs are independent and is essential for computing the
separability of compound models using the is_separable() function.
Having a separable compound model means that it can be decomposed into independent models,
which in turn is useful in many applications.
For example, it may be easier to define inverses using the independent parts of a model
than the entire model.
In other cases, tools using Generalized World Coordinate System (GWCS),
can be more flexible and take advantage of separable spectral and spatial transforms.
If a custom subclass of Model needs to override the
computation of its separability it can implement the
_calculate_separability_matrix method which should return the separability
matrix for that model.
Model Sets#
In some cases it is useful to describe many models of the same type but with
different sets of parameter values. This could be done simply by instantiating
as many instances of a Model as are needed. But that can
be inefficient for a large number of models. To that end, all model classes in
astropy.modeling can also be used to represent a model set which is a
collection of models of the same type, but with different values for their
parameters.
To instantiate a model set, use argument n_models=N where N is the
number of models in the set when constructing the model. The value of each
parameter must be a list or array of length N, such that each item in
the array corresponds to one model in the set:
>>> from astropy.modeling import models
>>> g = models.Gaussian1D(amplitude=[1, 2], mean=[0, 0],
... stddev=[0.1, 0.2], n_models=2)
>>> print(g)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 2
Parameters:
amplitude mean stddev
--------- ---- ------
1.0 0.0 0.1
2.0 0.0 0.2
This is equivalent to two Gaussians with the parameters amplitude=1, mean=0,
stddev=0.1 and amplitude=2, mean=0, stddev=0.2 respectively. When
printing the model the parameter values are displayed as a table, with each row
corresponding to a single model in the set.
The number of models in a model set can be determined using the len builtin:
>>> len(g)
2
Single models have a length of 1, and are not considered a model set as such.
When evaluating a model set, by default the input must be the same length as the number of models, with one input per model:
>>> g([0, 0.1])
array([1. , 1.76499381])
The result is an array with one result per model in the set. It is also possible to broadcast a single input value to all models in the set:
>>> g(0)
array([1., 2.])
Or when the input is an array:
>>> x = np.array([[0, 0, 0], [0.1, 0.1, 0.1]])
>>> print(x)
[[0. 0. 0. ]
[0.1 0.1 0.1]]
>>> g(x)
array([[1. , 1. , 1. ],
[1.76499381, 1.76499381, 1.76499381]])
Internally the shape of the inputs, outputs, and parameter values is controlled
by an attribute - model_set_axis. In the above case model_set_axis=0:
>>> g.model_set_axis
0
This indicates that elements along the 0-th axis will be passed as inputs to individual models. Sometimes it may be useful to pass inputs along a different axis, for example the 1st axis:
>>> x = np.array([[0, 0, 0], [0.1, 0.1, 0.1]]).T
>>> print(x)
[[0. 0.1]
[0. 0.1]
[0. 0.1]]
Because there are two models in this model set and we are passing three inputs along the 0th axis, evaluation will fail:
>>> g(x)
Traceback (most recent call last):
...
ValueError: Input argument 'x' does not have the correct dimensions in
model_set_axis=0 for a model set with n_models=2.
There are two ways to get around this. model_set_axis can be passed in
when the model is evaluated:
>>> g(x, model_set_axis=1)
array([[1. , 1.76499381],
[1. , 1.76499381],
[1. , 1.76499381]])
Or when the model is initialized:
>>> g = models.Gaussian1D(amplitude=[[1, 2]], mean=[[0, 0]],
... stddev=[[0.1, 0.2]], n_models=2,
... model_set_axis=1)
>>> g(x)
array([[1. , 1.76499381],
[1. , 1.76499381],
[1. , 1.76499381]])
Note that in the latter case, the shape of the individual parameters has changed to 2D because now the parameters are defined along the 1st axis.
The value of model_set_axis is either an integer number, representing the axis along which
the different parameter sets and inputs are defined, or a boolean of value False,
in which case it indicates all model sets should use the same inputs on evaluation.
For example, the above model has a value of 1 for model_set_axis.
If model_set_axis=False is passed the two models will be evaluated on the same input:
>>> g.model_set_axis
1
>>> result = g(x, model_set_axis=False)
>>> result
array([[[1. , 0.60653066],
[2. , 1.76499381]],
[[1. , 0.60653066],
[2. , 1.76499381]],
[[1. , 0.60653066],
[2. , 1.76499381]]])
>>> result[: , 0]
array([[1. , 0.60653066],
[1. , 0.60653066],
[1. , 0.60653066]])
>>> result[: , 1]
array([[2. , 1.76499381],
[2. , 1.76499381],
[2. , 1.76499381]])
Currently model sets are most useful for fitting a set of linear models (example) allowing a large number of models of the same type to be fitted simultaneously (and independently from each other) to some large set of inputs, such as fitting a polynomial to the time response of each pixel in a data cube. This can greatly speed up the fitting process. The speed-up is due to solving the set of equations to find the exact solution. Nonlinear models, which require an iterative algorithm, cannot be currently fit using model sets. Model sets of nonlinear models can only be evaluated.
When fitting model sets it is important that data arrays are passed to the fitter
in the correct shape. The shape depends on the model_set_axis attribute of the
model to be fit. The rule is that the index of the dependent variable that corresponds
to a model set should be along the model_set_axis dimension. For example, for a
1D model set with 3 models with model_set_axis == 1 the shape of y should be (x, 3):
>>> import numpy as np
>>> from astropy.modeling.models import Polynomial1D
>>> from astropy.modeling.fitting import LinearLSQFitter
>>> fitter = LinearLSQFitter()
>>> x = np.arange(4)
>>> y = np.array([2*x+1, x+4, x]).T
>>> print(y)
[[1 4 0]
[3 5 1]
[5 6 2]
[7 7 3]]
>>> print(y.shape)
(4, 3)
>>> m = Polynomial1D(1, n_models=3, model_set_axis=1)
>>> mfit = fitter(m, x, y)
For 2D models with 3 models and model_set_axis = 0 the shape of z should be (3, x, y):
>>> import numpy as np
>>> from astropy.modeling.models import Polynomial2D
>>> from astropy.modeling.fitting import LinearLSQFitter
>>> fitter = LinearLSQFitter()
>>> x = np.arange(8).reshape(2, 4)
>>> y = x
>>> z = np.asarray([2 * x + 1, x + 4, x + 3])
>>> print(z.shape)
(3, 2, 4)
>>> m = Polynomial2D(1, n_models=3, model_set_axis=0)
>>> mfit = fitter(m, x, y, z)
Model Serialization (Writing a Model to a File)#
Models are serializable using the ASDF format. This can be useful in many contexts, one of which is the implementation of a Generalized World Coordinate System (GWCS).
Serializing a model to disk is possible by assigning the object to AsdfFile.tree:
>>> from asdf import AsdfFile
>>> from astropy.modeling import models
>>> rotation = models.Rotation2D(angle=23.7)
>>> f = AsdfFile()
>>> f.tree['model'] = rotation
>>> f.write_to('rotation.asdf')
To read the file and create the model:
>>> import asdf
>>> with asdf.open('rotation.asdf') as f:
... model = f.tree['model']
>>> print(model)
Model: Rotation2D
Inputs: ('x', 'y')
Outputs: ('x', 'y')
Model set size: 1
Parameters:
angle
-----
23.7
Compound models can also be serialized. Please note that some model attributes (e.g meta,
tied parameter constraints used in fitting), as well as model sets are not yet serializable.
For more information on serialization of models, see The asdf-astropy Extension Package.
