GeneralSersic2D#
- class astropy.modeling.functional_models.GeneralSersic2D(amplitude=1, r_eff=1, n=4, x_0=0, y_0=0, ellip=0, theta=0.0, c=0, **kwargs)[source]#
Bases:
Sersic2DGeneralized two dimensional Sersic surface brightness profile that allows for “boxy” or “disky” (kite-like) isophote shapes.
- Parameters:
- amplitude
float Surface brightness at
r_eff.- r_eff
float Effective (half-light) radius.
- n
float Sersic index controlling the shape of the profile. Particular values of
nare equivalent to the following profiles:n=4 : de Vaucouleurs \(r^{1/4}\) profile
n=1 : Exponential profile
n=0.5 : Gaussian profile
- x_0
float, optional x position of the center.
- y_0
float, optional y position of the center.
- ellip
float, optional Ellipticity of the isophote, defined as 1.0 minus the ratio of the lengths of the semimajor and semiminor axes:
\[ellip = 1 - \frac{b}{a}\]- theta
floatorQuantity, optional The rotation angle as an angular quantity (
QuantityorAngle) or a value in radians (as a float). The rotation angle increases counterclockwise from the positive x axis.- c
float, optional Parameter controlling the shape of the generalized ellipses. Negative values correspond to disky (kite-like) isophotes and positive values correspond to boxy isophotes. Setting
c=0provides perfectly elliptical isophotes (the same model asSersic2D).
- amplitude
See also
Notes
Model formula:
\[I(x, y) = I_{e} \exp\left\{ -b_{n} \left[\left(\frac{r(x, y)}{r_{e}}\right)^{(1/n)} -1\right]\right\}\]where \(I_{e}\) is the
amplitude, \(r_{e}\) isreff, and \(r(x, y)\) is a rotated “generalized” ellipse (see Athanassoula et al. 1990) defined as:\[r(x, y)^2 = |A|^{c + 2} + \left(\frac{|B|}{1 - ellip}\right)^{c + 2}\]\[A = (x - x_0) \cos(\theta) + (y - y_0) \sin(\theta)\]\[B = -(x - x_0) \sin(\theta) + (y - y_0) \cos(\theta)\]The constant \(b_{n}\) is defined such that \(r_{e}\) contains half the total luminosity. It can be solved for numerically from the following equation:
\[\Gamma(2n) = 2\gamma (2n, b_{n})\]where \(\Gamma(a)\) is the gamma function and \(\gamma(a, x)\) is the lower incomplete gamma function.
References
Examples
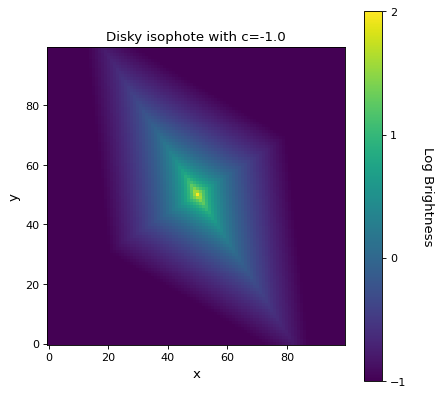
import numpy as np from astropy.modeling.models import GeneralSersic2D import matplotlib.pyplot as plt x, y = np.meshgrid(np.arange(100), np.arange(100)) mod = GeneralSersic2D(amplitude=1, r_eff=25, n=4, x_0=50, y_0=50, c=-1.0, ellip=0.5, theta=-1) img = mod(x, y) log_img = np.log10(img) fig, ax = plt.subplots() im = ax.imshow(log_img, origin='lower', interpolation='nearest', vmin=-1, vmax=2) cbar = fig.colorbar(im, ax=ax) cbar.set_label('Log Brightness', rotation=270, labelpad=25) cbar.set_ticks([-1, 0, 1, 2]) plt.title('Disky isophote with c=-1.0') plt.xlabel('x') plt.ylabel('y') plt.show()
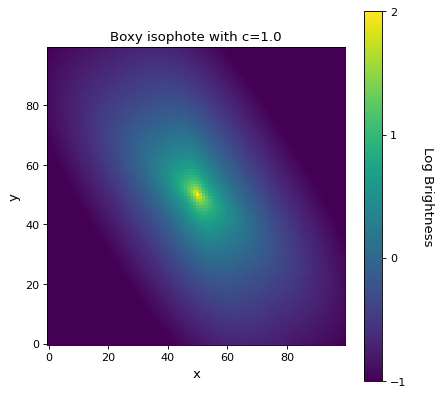
import numpy as np from astropy.modeling.models import GeneralSersic2D import matplotlib.pyplot as plt x, y = np.meshgrid(np.arange(100), np.arange(100)) mod = GeneralSersic2D(amplitude=1, r_eff=25, n=4, x_0=50, y_0=50, c=1.0, ellip=0.5, theta=-1) img = mod(x, y) log_img = np.log10(img) fig, ax = plt.subplots() im = ax.imshow(log_img, origin='lower', interpolation='nearest', vmin=-1, vmax=2) cbar = fig.colorbar(im, ax=ax) cbar.set_label('Log Brightness', rotation=270, labelpad=25) cbar.set_ticks([-1, 0, 1, 2]) plt.title('Boxy isophote with c=1.0') plt.xlabel('x') plt.ylabel('y') plt.show()
Attributes Summary
Names of the parameters that describe models of this type.
Attributes Documentation
- amplitude = Parameter('amplitude', value=1.0)#
- c = Parameter('c', value=0.0)#
- ellip = Parameter('ellip', value=0.0)#
- n = Parameter('n', value=4.0)#
- param_names = ('amplitude', 'r_eff', 'n', 'x_0', 'y_0', 'ellip', 'theta', 'c')#
Names of the parameters that describe models of this type.
The parameters in this tuple are in the same order they should be passed in when initializing a model of a specific type. Some types of models, such as polynomial models, have a different number of parameters depending on some other property of the model, such as the degree.
When defining a custom model class the value of this attribute is automatically set by the
Parameterattributes defined in the class body.
- r_eff = Parameter('r_eff', value=1.0)#
- theta = Parameter('theta', value=0.0)#
- x_0 = Parameter('x_0', value=0.0)#
- y_0 = Parameter('y_0', value=0.0)#
