Defining New Model Classes#
This document describes how to add a model to the package or to create a user-defined model. In short, one needs to define all model parameters and write a function which evaluates the model, that is, computes the mathematical function that implements the model. If the model is fittable, a function to compute the derivatives with respect to parameters is required if a linear fitting algorithm is to be used and optional if a non-linear fitter is to be used.
Basic custom models#
For most cases, the custom_model decorator provides an
easy way to make a new Model class from an existing Python
callable. The following example demonstrates how to set up a model consisting
of two Gaussians:
import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling.models import custom_model
from astropy.modeling.fitting import LevMarLSQFitter
# Define model
@custom_model
def sum_of_gaussians(x, amplitude1=1., mean1=-1., sigma1=1.,
amplitude2=1., mean2=1., sigma2=1.):
return (amplitude1 * np.exp(-0.5 * ((x - mean1) / sigma1)**2) +
amplitude2 * np.exp(-0.5 * ((x - mean2) / sigma2)**2))
# Generate fake data
rng = np.random.default_rng(0)
x = np.linspace(-5., 5., 200)
m_ref = sum_of_gaussians(amplitude1=2., mean1=-0.5, sigma1=0.4,
amplitude2=0.5, mean2=2., sigma2=1.0)
y = m_ref(x) + rng.normal(0., 0.1, x.shape)
# Fit model to data
m_init = sum_of_gaussians()
fit = LevMarLSQFitter()
m = fit(m_init, x, y)
# Plot the data and the best fit
plt.plot(x, y, 'o', color='k')
plt.plot(x, m(x))
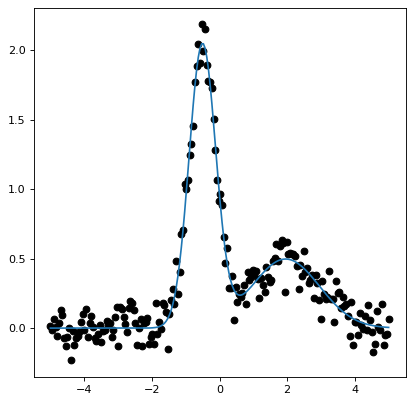
This decorator also supports setting a model’s
fit_deriv as well as creating models with
more than one inputs. Note that when creating a model from a function with
multiple outputs, the keyword argument n_outputs must be set to the
number of outputs of the function. It can also be used as a normal factory
function (for example SumOfGaussians = custom_model(sum_of_gaussians))
rather than as a decorator. See the custom_model
documentation for more examples.
A step by step definition of a 1-D Gaussian model#
The example described in Basic custom models can be used for most simple
cases, but the following section describes how to construct model classes in
general. Defining a full model class may be desirable, for example, to
provide more specialized parameters, or to implement special functionality not
supported by the basic custom_model factory function.
The details are explained below with a 1-D Gaussian model as an example. There
are two base classes for models. If the model is fittable, it should inherit
from FittableModel; if not it should subclass
Model.
If the model takes parameters they should be specified as class attributes in
the model’s class definition using the Parameter
descriptor. All arguments to the Parameter constructor are optional, and may
include a default value for that parameter, a text description of the parameter
(useful for help and documentation generation), as well default constraints
and custom getters/setters for the parameter value. It is also possible to
define a “validator” method for each parameter, enabling custom code to check
whether that parameter’s value is valid according to the model definition (for
example if it must be non-negative). See the example in
Parameter.validator for more details.
Note, that if pickling the model is important the validator function should be
assigned directly to the instance Parameter._validator instead of using
the decorator.
from astropy.modeling import Fittable1DModel, Parameter
class Gaussian1D(Fittable1DModel):
n_inputs = 1
n_outputs = 1
amplitude = Parameter()
mean = Parameter()
stddev = Parameter()
The n_inputs and n_outputs class attributes must be integers
indicating the number of independent variables that are input to evaluate the
model, and the number of outputs it returns. The labels of the inputs and
outputs, inputs and outputs, are generated automatically. It is possible
to overwrite the default ones by assigning the desired values in the class __init__
method, after calling super. outputs and inputs must be tuples of
strings with length n_outputs and n_inputs respectively.
Outputs may have the same labels as inputs (eg. inputs = ('x', 'y') and outputs = ('x', 'y')).
However, inputs must not conflict with each other (eg. inputs = ('x', 'x') is
incorrect) and likewise for outputs.
There are two helpful base classes in the modeling package that can be used to
avoid specifying n_inputs and n_outputs for most common models. These are
Fittable1DModel and Fittable2DModel.
For example, the actual Gaussian1D model is
a subclass of Fittable1DModel. This helps cut
down on boilerplate by not having to specify n_inputs, n_outputs, inputs
and outputs for many models (follow the link to Gaussian1D to see its source code, for
example).
Fittable models can be linear or nonlinear in a regression sense. The default
value of the linear attribute is False. Linear
models should define the linear class attribute as True. Because this
model is non-linear we can stick with the default.
Models which inherit from Fittable1DModel have the
Model._separable property already set to True.
All other models should define this property to indicate the
Model Separability.
Next, provide methods called evaluate to evaluate the model and
fit_deriv, to compute its derivatives with respect to parameters. These
may be normal methods, classmethod, or staticmethod, though the convention
is to use staticmethod when the function does not depend on any of the
object’s other attributes (i.e., it does not reference self) or any of the
class’s other attributes as in the case of classmethod. The evaluation
method takes all input coordinates as separate arguments and all of the model’s
parameters in the same order they would be listed by
param_names.
For this example:
@staticmethod
def evaluate(x, amplitude, mean, stddev):
return amplitude * np.exp((-(1 / (2. * stddev**2)) * (x - mean)**2))
It should be made clear that the evaluate method must be designed to take
the model’s parameter values as arguments. This may seem at odds with the fact
that the parameter values are already available via attribute of the model
(eg. model.amplitude). However, passing the parameter values directly to
evaluate is a more efficient way to use it in many cases, such as fitting.
Users of your model would not generally use evaluate directly. Instead
they create an instance of the model and call it on some input. The
__call__ method of models uses evaluate internally, but users do not
need to be aware of it. The default __call__ implementation also handles
details such as checking that the inputs are correctly formatted and follow
Numpy’s broadcasting rules before attempting to evaluate the model.
Like evaluate, the fit_deriv method takes as input all coordinates and
all parameter values as arguments. There is an option to compute numerical
derivatives for nonlinear models in which case the fit_deriv method should
be None:
@staticmethod
def fit_deriv(x, amplitude, mean, stddev):
d_amplitude = np.exp(- 0.5 / stddev**2 * (x - mean)**2)
d_mean = (amplitude *
np.exp(- 0.5 / stddev**2 * (x - mean)**2) *
(x - mean) / stddev**2)
d_stddev = (2 * amplitude *
np.exp(- 0.5 / stddev**2 * (x - mean)**2) *
(x - mean)**2 / stddev**3)
return [d_amplitude, d_mean, d_stddev]
Note that we did not have to define an __init__ method or a __call__
method for our model. For most models the __init__ follows the same pattern,
taking the parameter values as positional arguments, followed by several optional
keyword arguments (constraints, etc.). The modeling framework automatically generates an
__init__ for your class that has the correct calling signature (see for
yourself by calling help(Gaussian1D.__init__) on the example model we just
defined).
There are cases where it might be desirable to define a custom __init__.
For example, the Gaussian2D model takes
an optional cov_matrix argument which can be used as an alternative way to
specify the x/y_stddev and theta parameters. This is perfectly valid so long
as the __init__ determines appropriate values for the actual parameters and
then calls the super __init__ with the standard arguments. Schematically
this looks something like:
def __init__(self, amplitude, x_mean, y_mean, x_stddev=None,
y_stddev=None, theta=None, cov_matrix=None, **kwargs):
# The **kwargs here should be understood as other keyword arguments
# accepted by the basic Model.__init__ (such as constraints)
if cov_matrix is not None:
# Set x/y_stddev and theta from the covariance matrix
x_stddev = ...
y_stddev = ...
theta = ...
# Don't pass on cov_matrix since it doesn't mean anything to the base
# class
super().__init__(amplitude, x_mean, y_mean, x_stddev, y_stddev, theta,
**kwargs)
Full example#
import numpy as np
from astropy.modeling import Fittable1DModel, Parameter
class Gaussian1D(Fittable1DModel):
amplitude = Parameter()
mean = Parameter()
stddev = Parameter()
@staticmethod
def evaluate(x, amplitude, mean, stddev):
return amplitude * np.exp((-(1 / (2. * stddev**2)) * (x - mean)**2))
@staticmethod
def fit_deriv(x, amplitude, mean, stddev):
d_amplitude = np.exp((-(1 / (stddev**2)) * (x - mean)**2))
d_mean = (2 * amplitude *
np.exp((-(1 / (stddev**2)) * (x - mean)**2)) *
(x - mean) / (stddev**2))
d_stddev = (2 * amplitude *
np.exp((-(1 / (stddev**2)) * (x - mean)**2)) *
((x - mean)**2) / (stddev**3))
return [d_amplitude, d_mean, d_stddev]
A full example of a LineModel#
This example demonstrates one other optional feature for model classes, which
is an inverse. An inverse implementation should be
a property that returns a new model instance (not necessarily of the same
class as the model being inverted) that computes the inverse of that model, so
that for some model instance with an inverse, model.inverse(model(*input)) ==
input.
import numpy as np
from astropy.modeling import Fittable1DModel, Parameter
class LineModel(Fittable1DModel):
slope = Parameter()
intercept = Parameter()
linear = True
@staticmethod
def evaluate(x, slope, intercept):
return slope * x + intercept
@staticmethod
def fit_deriv(x, slope, intercept):
d_slope = x
d_intercept = np.ones_like(x)
return [d_slope, d_intercept]
@property
def inverse(self):
new_slope = self.slope ** -1
new_intercept = -self.intercept / self.slope
return LineModel(slope=new_slope, intercept=new_intercept)
Note
The above example is essentially equivalent to the built-in
Linear1D model.
