Time Series (astropy.timeseries)#
Introduction#
From sampling a continuous variable at fixed times to counting events binned
into time windows, many different areas of astrophysics require the manipulation
of 1D time series data. To address this need, the astropy.timeseries
subpackage provides classes to represent and manipulate time series.
The time series classes presented below are QTable subclasses that have
special columns to represent times using the Time class. Therefore, much of
the functionality described in Data Tables (astropy.table) applies here. But the main
purpose of the new classes are to provide time series-specific functionality
above and beyond QTable.
Getting Started#
In this section, we take a quick look at how to read in a time series, access the data, and carry out some basic analysis. For more details about creating and using time series, see the full documentation in Using timeseries.
The most basic time series class is TimeSeries — it represents a time series
as a collection of values at specific points in time. If you are interested in
representing time series as measurements in discrete time bins, you will likely
be interested in the BinnedTimeSeries subclass which we show in
Using timeseries).
To start off, we retrieve a FITS file containing a Kepler light curve for a source:
>>> from astropy.utils.data import get_pkg_data_filename
>>> filename = get_pkg_data_filename('timeseries/kplr010666592-2009131110544_slc.fits')
Note
The light curve provided here is handpicked for example purposes. For more information about the Kepler FITS format, see Section 2.3.1 of the Kepler Archive Manual. To get other light curves for science purposes using Python, see the astroquery affiliated package.
We can then use the TimeSeries class to read in this file:
>>> from astropy.timeseries import TimeSeries
>>> ts = TimeSeries.read(filename, format='kepler.fits')
Time series are specialized kinds of Table objects:
>>> ts
<TimeSeries length=14280>
time timecorr ... pos_corr1 pos_corr2
d ... pix pix
Time float32 ... float32 float32
----------------------- ------------- ... -------------- --------------
2009-05-02T00:41:40.338 6.630610e-04 ... 1.5822421e-03 -1.4463664e-03
2009-05-02T00:42:39.188 6.630857e-04 ... 1.5743829e-03 -1.4540013e-03
2009-05-02T00:43:38.045 6.631103e-04 ... 1.5665225e-03 -1.4616371e-03
2009-05-02T00:44:36.894 6.631350e-04 ... 1.5586632e-03 -1.4692718e-03
2009-05-02T00:45:35.752 6.631597e-04 ... 1.5508028e-03 -1.4769078e-03
2009-05-02T00:46:34.601 6.631844e-04 ... 1.5429436e-03 -1.4845425e-03
2009-05-02T00:47:33.451 6.632091e-04 ... 1.5350844e-03 -1.4921773e-03
2009-05-02T00:48:32.291 6.632337e-04 ... 1.5272264e-03 -1.4998110e-03
2009-05-02T00:49:31.149 6.632584e-04 ... 1.5193661e-03 -1.5074468e-03
... ... ... ... ...
2009-05-11T17:58:22.526 1.014493e-03 ... 3.6121816e-03 3.1950327e-03
2009-05-11T17:59:21.376 1.014518e-03 ... 3.6102540e-03 3.1872767e-03
2009-05-11T18:00:20.225 1.014542e-03 ... 3.6083264e-03 3.1795206e-03
2009-05-11T18:01:19.065 1.014567e-03 ... 3.6063993e-03 3.1717657e-03
2009-05-11T18:02:17.923 1.014591e-03 ... 3.6044715e-03 3.1640085e-03
2009-05-11T18:03:16.772 1.014615e-03 ... 3.6025438e-03 3.1562524e-03
2009-05-11T18:04:15.630 1.014640e-03 ... 3.6006160e-03 3.1484952e-03
2009-05-11T18:05:14.479 1.014664e-03 ... 3.5986886e-03 3.1407392e-03
2009-05-11T18:06:13.328 1.014689e-03 ... 3.5967610e-03 3.1329831e-03
2009-05-11T18:07:12.186 1.014713e-03 ... 3.5948332e-03 3.1252259e-03
In the same way as for Table objects, the various columns and rows of
TimeSeries objects can be accessed and sliced using index notation:
>>> ts['sap_flux']
<Quantity [1027045.06, 1027184.44, 1027076.25, ..., 1025451.56, 1025468.5 ,
1025930.9 ] electron / s>
>>> ts['time', 'sap_flux']
<TimeSeries length=14280>
time sap_flux
electron / s
Time float32
----------------------- --------------
2009-05-02T00:41:40.338 1.0270451e+06
2009-05-02T00:42:39.188 1.0271844e+06
2009-05-02T00:43:38.045 1.0270762e+06
2009-05-02T00:44:36.894 1.0271414e+06
2009-05-02T00:45:35.752 1.0271569e+06
2009-05-02T00:46:34.601 1.0272296e+06
2009-05-02T00:47:33.451 1.0273199e+06
2009-05-02T00:48:32.291 1.0271497e+06
2009-05-02T00:49:31.149 1.0271755e+06
... ...
2009-05-11T17:58:22.526 1.0234769e+06
2009-05-11T17:59:21.376 1.0234574e+06
2009-05-11T18:00:20.225 1.0238128e+06
2009-05-11T18:01:19.065 1.0243234e+06
2009-05-11T18:02:17.923 1.0244257e+06
2009-05-11T18:03:16.772 1.0248654e+06
2009-05-11T18:04:15.630 1.0250156e+06
2009-05-11T18:05:14.479 1.0254516e+06
2009-05-11T18:06:13.328 1.0254685e+06
2009-05-11T18:07:12.186 1.0259309e+06
>>> ts[0:4]
<TimeSeries length=4>
time timecorr ... pos_corr1 pos_corr2
d ... pix pix
Time float32 ... float32 float32
----------------------- ------------- ... -------------- --------------
2009-05-02T00:41:40.338 6.630610e-04 ... 1.5822421e-03 -1.4463664e-03
2009-05-02T00:42:39.188 6.630857e-04 ... 1.5743829e-03 -1.4540013e-03
2009-05-02T00:43:38.045 6.631103e-04 ... 1.5665225e-03 -1.4616371e-03
2009-05-02T00:44:36.894 6.631350e-04 ... 1.5586632e-03 -1.4692718e-03
As seen in the previous examples, TimeSeries objects have a time
column, which is always the first column. This column can also be accessed using
the .time attribute:
>>> ts.time
<Time object: scale='tdb' format='isot' value=['2009-05-02T00:41:40.338' '2009-05-02T00:42:39.188'
'2009-05-02T00:43:38.045' ... '2009-05-11T18:05:14.479'
'2009-05-11T18:06:13.328' '2009-05-11T18:07:12.186']>
The first column is always a Time object (see Times and Dates), which therefore supports the ability to convert to different
time scales and formats:
>>> ts.time.mjd
array([54953.0289391 , 54953.02962023, 54953.03030145, ...,
54962.7536398 , 54962.75432093, 54962.75500215])
>>> ts.time.unix
array([1.24122483e+09, 1.24122489e+09, 1.24122495e+09, ...,
1.24206505e+09, 1.24206511e+09, 1.24206517e+09])
We can also check what time scale the time is defined on:
>>> ts.time.scale
'tdb'
This is the Barycentric Dynamical Time scale (see Time and Dates (astropy.time) for more details). We can use what we have seen so far to make a plot:
import matplotlib.pyplot as plt
plt.plot(ts.time.jd, ts['sap_flux'], 'k.', markersize=1)
plt.xlabel('Julian Date')
plt.ylabel('SAP Flux (e-/s)')
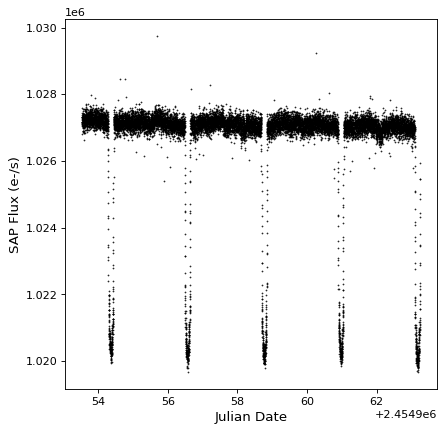
It looks like there are a few transits! We can use the
BoxLeastSquares class to estimate the
period, using the “box least squares” (BLS) algorithm:
>>> import numpy as np
>>> from astropy import units as u
>>> from astropy.timeseries import BoxLeastSquares
>>> periodogram = BoxLeastSquares.from_timeseries(ts, 'sap_flux')
To run the periodogram analysis, we use a box with a duration of 0.2 days:
>>> results = periodogram.autopower(0.2 * u.day)
>>> best = np.argmax(results.power)
>>> period = results.period[best]
>>> period
<Quantity 2.20551724 d>
>>> transit_time = results.transit_time[best]
>>> transit_time
<Time object: scale='tdb' format='isot' value=2009-05-02T20:51:16.338>
For more information on available periodogram algorithms, see Periodogram Algorithms.
We can now fold the time series using the period we found above using the
fold() method:
>>> ts_folded = ts.fold(period=period, epoch_time=transit_time)
Now we can take a look at the folded time series:
plt.plot(ts_folded.time.jd, ts_folded['sap_flux'], 'k.', markersize=1)
plt.xlabel('Time (days)')
plt.ylabel('SAP Flux (e-/s)')
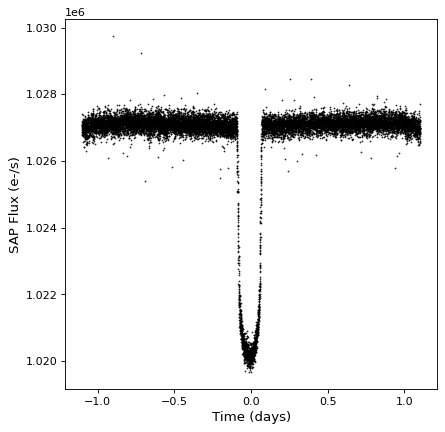
Using the Astrostatistics Tools (astropy.stats) module, we can normalize the flux by sigma-clipping the data to determine the baseline flux:
>>> from astropy.stats import sigma_clipped_stats
>>> mean, median, stddev = sigma_clipped_stats(ts_folded['sap_flux'])
>>> ts_folded['sap_flux_norm'] = ts_folded['sap_flux'] / median
And we can downsample the time series by binning the points into bins of equal
time — this returns a BinnedTimeSeries:
>>> from astropy.timeseries import aggregate_downsample
>>> ts_binned = aggregate_downsample(ts_folded, time_bin_size=0.03 * u.day)
>>> ts_binned
<BinnedTimeSeries length=74>
time_bin_start time_bin_size ... pos_corr2 sap_flux_norm
d ... pix
TimeDelta float64 ... float64 float64
------------------- ------------- ... ----------------------- ------------------
-1.1022116370482966 0.03 ... 0.00031207725987769663 0.9998741745948792
-1.0722116370482966 0.03 ... 0.00041217938996851444 0.9999074339866638
-1.0422116370482966 0.03 ... 0.00039273229776881635 0.999972939491272
-1.0122116370482965 0.03 ... 0.0002928022004198283 1.0000077486038208
-0.9822116370482965 0.03 ... 0.0003891147789545357 0.9999921917915344
-0.9522116370482965 0.03 ... 0.0003491091774776578 1.0000101327896118
-0.9222116370482966 0.03 ... 0.0002824827388394624 1.0000121593475342
-0.8922116370482965 0.03 ... 0.00016335179680027068 0.9999905228614807
-0.8622116370482965 0.03 ... 0.0001397567830281332 1.0000263452529907
... ... ... ... ...
0.817788362951705 0.03 ... -2.2798192730988376e-05 1.0000624656677246
0.847788362951705 0.03 ... 0.00022221534163691103 1.0000633001327515
0.877788362951705 0.03 ... 0.00019213277846574783 1.0000433921813965
0.9077883629517051 0.03 ... 0.0002187517675338313 1.000024676322937
0.9377883629517049 0.03 ... 0.00016979355132207274 1.0000224113464355
0.9677883629517047 0.03 ... 0.00014231358363758773 1.0000698566436768
0.9977883629517045 0.03 ... 0.0001224415173055604 0.9999606013298035
1.0277883629517042 0.03 ... 0.00027701034559868276 0.9999635815620422
1.057788362951704 0.03 ... 0.0003093520936090499 0.9999105930328369
1.0877883629517038 0.03 ... 0.00022884277859702706 0.9998687505722046
Now we can take a look at the final result:
plt.plot(ts_folded.time.jd, ts_folded['sap_flux_norm'], 'k.', markersize=1)
plt.plot(ts_binned.time_bin_start.jd, ts_binned['sap_flux_norm'], 'r-', drawstyle='steps-post')
plt.xlabel('Time (days)')
plt.ylabel('Normalized flux')
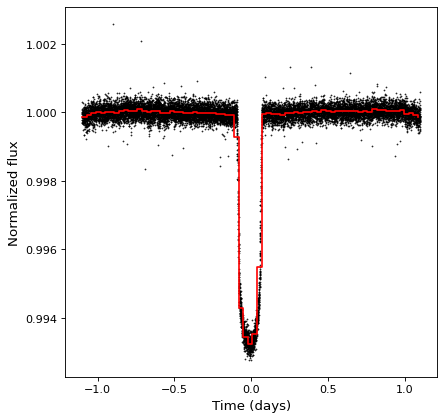
To learn more about the capabilities in the astropy.timeseries module, you can
find links to the full documentation in the next section.
Using timeseries#
The details of using astropy.timeseries are provided in the following
sections:
