Working with Angles#
The angular components of the various coordinate objects are represented
by objects of the Angle class. While most likely to be encountered in
the context of coordinate objects, Angle objects can also be used on
their own wherever a representation of an angle is needed.
Creation#
The creation of an Angle object is quite flexible and supports a wide
variety of input object types and formats. The type of the input angle(s)
can be array, scalar, tuple, string, Quantity or another
Angle. This is best illustrated with a number of examples of valid ways
to create an Angle.
Examples#
There are a number of ways to create an Angle:
>>> import numpy as np
>>> from astropy import units as u
>>> from astropy.coordinates import Angle
>>> Angle('10.2345d') # String with 'd' abbreviation for degrees
<Angle 10.2345 deg>
>>> Angle(['10.2345d', '-20d']) # Array of strings
<Angle [ 10.2345, -20. ] deg>
>>> Angle('1:2:30.43 degrees') # Sexagesimal degrees
<Angle 1.04178611 deg>
>>> Angle('1 2 0 hours') # Sexagesimal hours
<Angle 1.03333333 hourangle>
>>> Angle(np.arange(1., 8.), unit=u.deg) # Numpy array from 1..7 in degrees
<Angle [1., 2., 3., 4., 5., 6., 7.] deg>
>>> Angle('1°2′3″') # Unicode degree, arcmin and arcsec symbols
<Angle 1.03416667 deg>
>>> Angle('1°2′3″N') # Unicode degree, arcmin, arcsec symbols and direction
<Angle 1.03416667 deg>
>>> Angle('1d2m3.4s') # Degree, arcmin, arcsec.
<Angle 1.03427778 deg>
>>> Angle('1d2m3.4sS') # Degree, arcmin, arcsec, direction.
<Angle -1.03427778 deg>
>>> Angle('-1h2m3s') # Hour, minute, second
<Angle -1.03416667 hourangle>
>>> Angle('-1h2m3sW') # Hour, minute, second, direction
<Angle 1.03416667 hourangle>
>>> Angle(10.2345 * u.deg) # From a Quantity object in degrees
<Angle 10.2345 deg>
>>> Angle(Angle(10.2345 * u.deg)) # From another Angle object
<Angle 10.2345 deg>
Representation#
The Angle object also supports a variety of ways of representing the value
of the angle, both as a floating point number and as a string.
Examples#
There are many ways to represent the value of an Angle:
>>> a = Angle(1, u.radian)
>>> a
<Angle 1. rad>
>>> a.radian
1.0
>>> a.degree
57.29577951308232
>>> a.hour
3.8197186342054885
>>> a.hms
hms_tuple(h=3.0, m=49.0, s=10.987083139758766)
>>> a.dms
dms_tuple(d=57.0, m=17.0, s=44.806247096362313)
>>> a.signed_dms
signed_dms_tuple(sign=1.0, d=57.0, m=17.0, s=44.806247096362313)
>>> (-a).dms
dms_tuple(d=-57.0, m=-17.0, s=-44.806247096362313)
>>> (-a).signed_dms
signed_dms_tuple(sign=-1.0, d=57.0, m=17.0, s=44.806247096362313)
>>> a.arcminute
3437.7467707849396
>>> f"{a}"
'1.0 rad'
>>> f"{a:latex}"
'$1\\;\\mathrm{rad}$'
>>> f"{a.to(u.deg):latex}"
'$57^\\circ17{}^\\prime44.8062471{}^{\\prime\\prime}$'
>>> a.to_string()
'1 rad'
>>> a.to_string(unit=u.degree)
'57d17m44.8062471s'
>>> a.to_string(unit=u.degree, sep=':')
'57:17:44.8062471'
>>> a.to_string(unit=u.degree, sep=('deg', 'm', 's'))
'57deg17m44.8062471s'
>>> a.to_string(unit=u.hour)
'3h49m10.98708314s'
>>> a.to_string(unit=u.hour, decimal=True)
'3.81972'
Usage#
Angles will also behave correctly for appropriate arithmetic operations.
Example#
To use Angle objects in arithmetic operations:
>>> a = Angle(1.0, u.radian)
>>> a + 0.5 * u.radian + 2 * a
<Angle 3.5 rad>
>>> np.sin(a / 2)
<Quantity 0.47942554>
>>> a == a
array(True, dtype=bool)
>>> a == (a + a)
array(False, dtype=bool)
Angle objects can also be used for creating coordinate objects.
Example#
To create a coordinate object using an Angle:
>>> from astropy.coordinates import ICRS
>>> ICRS(Angle(1, u.deg), Angle(0.5, u.deg))
<ICRS Coordinate: (ra, dec) in deg
(1., 0.5)>
Wrapping and Bounds#
There are two utility methods for working with angles that should have bounds.
The wrap_at() method allows taking an angle or
angles and wrapping to be within a single 360 degree slice. The
is_within_bounds() method returns a
boolean indicating whether an angle or angles is within the specified bounds.
Note
While creating Angle instances from arrays with integral data types
is technically possible (for example with dtype=int), it is very
limited in functionality and in particular wrapping is not supported for
such objects.
Longitude and Latitude Objects#
Longitude and Latitude are two specialized subclasses of the Angle
class that are used for all of the spherical coordinate classes.
Longitude is used to represent values like right ascension, Galactic
longitude, and azimuth (for Equatorial, Galactic, and Alt-Az coordinates,
respectively). Latitude is used for declination, Galactic latitude, and
elevation.
Longitude#
A Longitude object is distinguished from a pure Angle by virtue of a
wrap_angle property. The wrap_angle specifies that all angle values
represented by the object will be in the range:
wrap_angle - 360 * u.deg <= angle(s) < wrap_angle
The default wrap_angle is 360 deg. Setting 'wrap_angle=180 * u.deg'
would instead result in values between -180 and +180 deg. Setting the
wrap_angle attribute of an existing Longitude object will result in
re-wrapping the angle values in-place. For example:
>>> from astropy.coordinates import Longitude
>>> a = Longitude([-20, 150, 350, 360] * u.deg)
>>> a.degree
array([340., 150., 350., 0.])
>>> a.wrap_angle = 180 * u.deg
>>> a.degree
array([-20., 150., -10., 0.])
Latitude#
A Latitude object is distinguished from a pure Angle by virtue
of being bounded so that:
-90.0 * u.deg <= angle(s) <= +90.0 * u.deg
Any attempt to set a value outside of that range will result in a
ValueError.
Generating Angle Values#
Astropy provides utility functions for generating angular or spherical
positions, either with random sampling or with a grid of values. These functions
all return BaseRepresentation subclass instances, which
can be passed directly into coordinate frame classes or SkyCoord to create
random or gridded coordinate objects.
With Random Sampling#
These functions both use standard, random spherical point picking to generate angular
positions that are uniformly distributed on the surface of the unit sphere. To
retrieve angular values only, use
uniform_spherical_random_surface. For
example, to generate 4 random angular positions:
>>> from astropy.coordinates import uniform_spherical_random_surface
>>> pts = uniform_spherical_random_surface(size=4)
>>> pts
<UnitSphericalRepresentation (lon, lat) in rad
[(0.52561028, 0.38712031), (0.29900285, 0.52776066),
(0.98199282, 0.34247723), (2.15260367, 1.01499232)]>
To generate three-dimensional positions uniformly within a spherical volume set
by a maximum radius, instead use the
uniform_spherical_random_volume
function. For example, to generate 4 random 3D positions:
>>> from astropy.coordinates import uniform_spherical_random_volume
>>> pts_3d = uniform_spherical_random_volume(size=4)
>>> pts_3d
<SphericalRepresentation (lon, lat, distance) in (rad, rad, )
[(4.98504602, -0.74247419, 0.39752416),
(5.53281607, 0.89425191, 0.7391255 ),
(0.88100456, 0.21080555, 0.5531785 ),
(6.00879324, 0.61547168, 0.61746148)]>
By default, the distance values returned are uniformly distributed within the
unit sphere (i.e., the distance values are dimensionless). To instead generate
random points within a sphere of a given dimensional radius, for example, 1
parsec, pass in a Quantity object with the max_radius argument:
>>> import astropy.units as u
>>> pts_3d = uniform_spherical_random_volume(size=4, max_radius=2*u.pc)
>>> pts_3d
<SphericalRepresentation (lon, lat, distance) in (rad, rad, pc)
[(3.36590297, -0.23085809, 1.47210093),
(6.14591179, 0.06840621, 0.9325143 ),
(2.19194797, 0.55099774, 1.19294064),
(5.25689272, -1.17703409, 1.63773358)]>
On a Grid#
No grid or lattice of points on the sphere can produce equal spacing between all grid points, but many approximate algorithms exist for generating angular grids with nearly even spacing (for example, see this page).
One simple and popular method in this context is the golden spiral method, which is available in
astropy.coordinates through the utility function
golden_spiral_grid. This function accepts
a single argument, size, which specifies the number of points to generate in
the grid:
>>> from astropy.coordinates import golden_spiral_grid
>>> golden_pts = golden_spiral_grid(size=32)
>>> golden_pts
<UnitSphericalRepresentation (lon, lat) in rad
[(1.94161104, 1.32014066), (5.82483312, 1.1343273 ),
(3.42486989, 1.004232 ), (1.02490666, 0.89666582),
(4.90812873, 0.80200278), (2.5081655 , 0.71583806),
(0.10820227, 0.63571129), (3.99142435, 0.56007531),
(1.59146112, 0.48787515), (5.4746832 , 0.41834639),
(3.07471997, 0.35090734), (0.67475674, 0.28509644),
(4.55797882, 0.22053326), (2.15801559, 0.15689287),
(6.04123767, 0.09388788), (3.64127444, 0.03125509),
(1.24131121, -0.03125509), (5.12453328, -0.09388788),
(2.72457005, -0.15689287), (0.32460682, -0.22053326),
(4.2078289 , -0.28509644), (1.80786567, -0.35090734),
(5.69108775, -0.41834639), (3.29112452, -0.48787515),
(0.89116129, -0.56007531), (4.77438337, -0.63571129),
(2.37442014, -0.71583806), (6.25764222, -0.80200278),
(3.85767899, -0.89666582), (1.45771576, -1.004232 ),
(5.34093783, -1.1343273 ), (2.9409746 , -1.32014066)]>
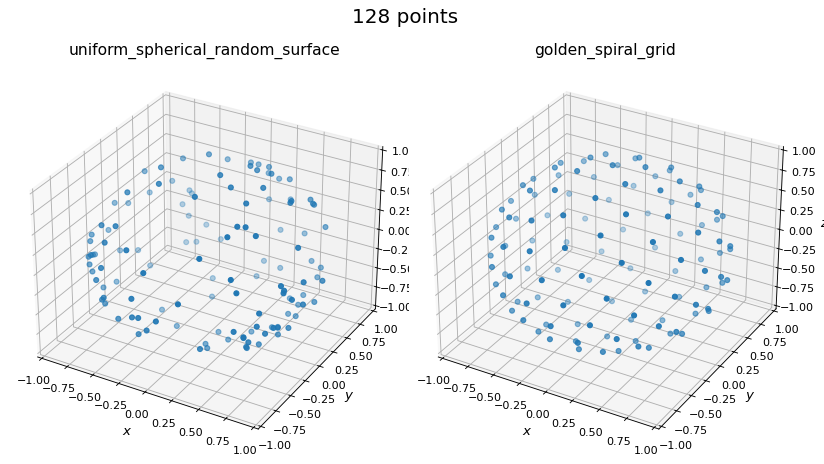
Comparing Spherical Point Generation Methods#