Ripley’s K Function Estimators#
Spatial correlation functions have been used in the astronomical context to estimate the probability of finding an object (e.g., a galaxy) within a given distance of another object [1].
Ripley’s K function is a type of estimator used to characterize the correlation
of such spatial point processes
[2], [3], [4], [5], [6].
More precisely, it describes correlation among objects in a given field.
The RipleysKEstimator class implements some
estimators for this function which provides several methods for
edge effects correction.
Basic Usage#
The actual implementation of Ripley’s K function estimators lie in the method
evaluate, which take the following arguments: data, radii, and
optionally, mode.
The data argument is a 2D array which represents the set of observed
points (events) in the area of study. The radii argument corresponds to a
set of distances for which the estimator will be evaluated. The mode
argument takes a value on the following linguistic set
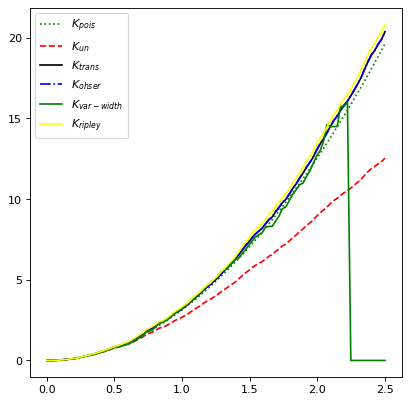
{none, translation, ohser, var-width, ripley}; each keyword represents a
different method to perform correction due to edge effects. See the API
documentation and references for details about these methods.
Instances of RipleysKEstimator can also be used as
callables (which is equivalent to calling the evaluate method).
Example#
To use Ripley’s K Function Estimators from astropy’s stats sub-package:
import numpy as np
from matplotlib import pyplot as plt
from astropy.stats import RipleysKEstimator
rng = np.random.default_rng()
z = rng.uniform(low=5, high=10, size=(100, 2))
Kest = RipleysKEstimator(area=25, x_max=10, y_max=10, x_min=5, y_min=5)
r = np.linspace(0, 2.5, 100)
plt.plot(r, Kest.poisson(r), color='green', ls=':', label=r'$K_{pois}$')
plt.plot(r, Kest(data=z, radii=r, mode='none'), color='red', ls='--',
label=r'$K_{un}$')
plt.plot(r, Kest(data=z, radii=r, mode='translation'), color='black',
label=r'$K_{trans}$')
plt.plot(r, Kest(data=z, radii=r, mode='ohser'), color='blue', ls='-.',
label=r'$K_{ohser}$')
plt.plot(r, Kest(data=z, radii=r, mode='var-width'), color='green',
label=r'$K_{var-width}$')
plt.plot(r, Kest(data=z, radii=r, mode='ripley'), color='yellow',
label=r'$K_{ripley}$')
plt.legend()